论文题目：AdaptiveKalman-InformedTransformer

创新点

常规 EKF 通常把 Q 设成常数；但真实中模型误差会随时间和运动状态变化。A-KIT 用 Kalman-Informed Transformer 根据当前状态和观测在线估计Q，再交给 EKF 用，这样在过程噪声变化时仍能保持较好的融合效果

如何实现

用「自适应估计的 Q̂」+「可学习的网络 A-KIT」得到更好的 Q（即 Q^A-KIT），再把这个 Q 用在卡尔曼里，并通过一个和真值有关的损失来训练这个网络。

特点：保持 EKF 的可解释性与滤波结构，用深度学习解决 Q 难以人工标定、时变的问题

A-KIT 与卡尔曼滤波的整体流程

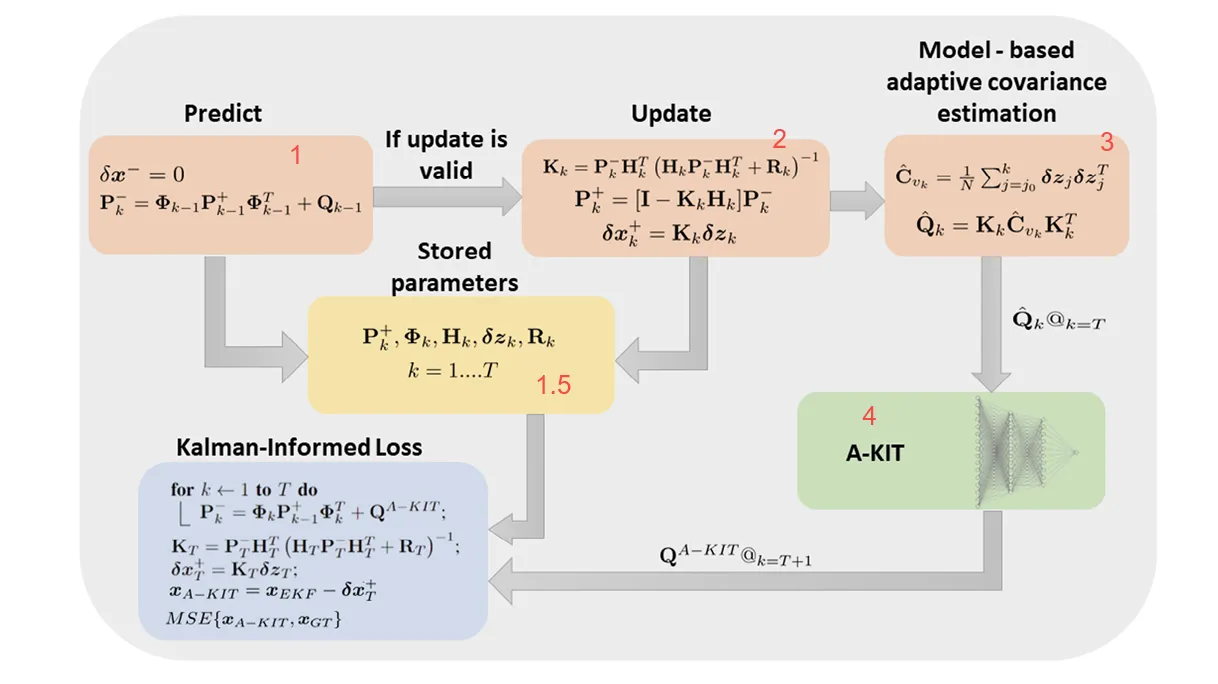
框1+框2：标准EKF步骤

EKF的标准过程：预测和更新

\begin{aligned} & x_k^{-}=f\left(\hat{x}_{k-1}, U_{k-1}, 0\right) \\ & P_k^{-}=A P_{k-1} A^T+W Q W^T \\ & K_k=\left(P_k^{-} H^T\right) /\left(H P_k^{-} H^T+V R V^T\right) \\ & \hat{x}_k=x_k^{-}+K_k\left(z_k-h\left(x_k^{-}, 0\right)\right) \\ & P_k=\left(I-K_k H\right) P_k^{-} \end{aligned}

框1.5：存储每一步EKF产生的变量

$P_k^{+}, \Phi_k, H_k, \delta z_k, R_k$ 等变量都存下来了

框3：基于模型的自适应协方差估计

目的：不事先给定 Q，而是从这段轨迹的观测残差（新息）里，反推过程噪声大概多大，得到一个 Q 的估计

观测残差（新息）即观测和预测的差

\Delta z_k=z_k-H_k\hat{x_k}^-

若模型/过程噪声很大：预测容易偏， $\Delta z_k$ 会偏大、波动大。
若模型很准、过程噪声小: $\Delta z_k$ 会小、更稳定。
$\Delta z_k$ 的协方差里，藏着「过程噪声有多大」的信息。

所以用存下来的 $\Delta z_j$ 估计新息协方差：

\hat{C}_{v_k}=\frac{1}{N} \sum_j \delta z_j \delta z_j^T

用卡尔曼增益 $K_k$ 和 $\mathrm{C}_{v_k}$ 得到 Q 的估计:

Q_k=K_k A_{v_k} K_k^T

在 k=T 时，把 $Q_T$ 送给 A-KIT，作为「这段轨迹反映出的 Q」

自适应协方差估计 = 用这段轨迹的 $\Delta z_j$ 统计，反推过程噪声 Q，得到 $\hat{Q}_k$ 。

框4：A-KIT网络——从 Q̂ 和传感器到 Q^A-KIT

下图描述了 QA-KIT 这个神经网络是怎么从传感器数据得到过程噪声协方差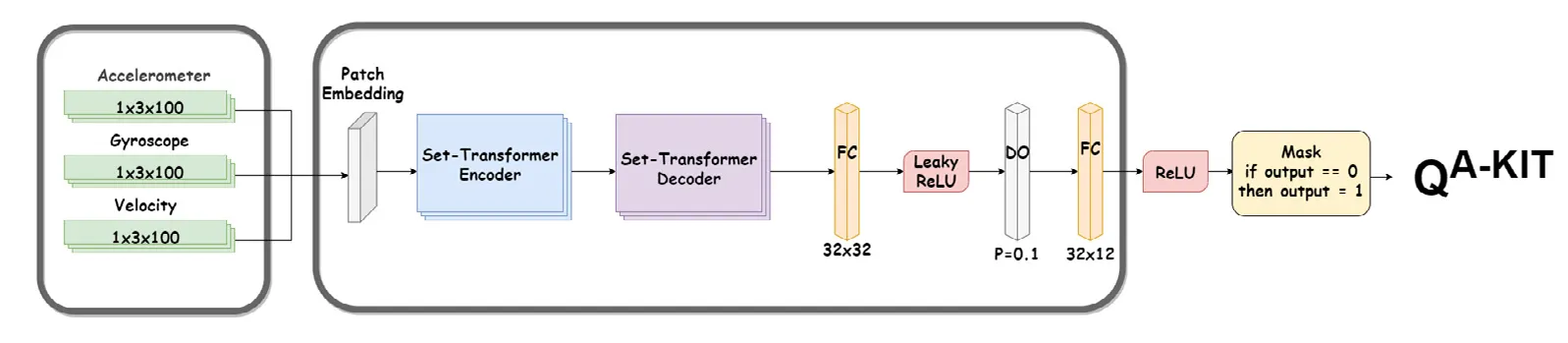输入：三种传感器序列，维度均为 1×3×100

加速度计 (Accelerometer)
陀螺仪 (Gyroscope)
速度 (Velocity)

结合图1，A-KIT网络还接收了噪声估计值 $\hat{Q}_k$

代码中的对应关系

bash
展开代码
Network.forward(self, x, Q)

x：经过 Patch Embedding + Set-Transformer + FC，对应传感器/序列数据；
Q：在最后一步用 Q[:, :, :, -2] 参与运算，对应估计的过程噪声（例如自适应估计得到的 $Q̂$ ）

主干：

Patch Embedding：把原始序列切成“补丁”并做嵌入
Set-Transformer Encoder / Decoder：对集合/序列做编码-解码，得到高层表示
全连接 + 激活：FC → Leaky ReLU → Dropout(0.1) → FC → ReLU，把表示映射到需要的维度

正确的缩放往往依赖整段序列的模式，而不是某一帧或某一个局部

bash
展开代码
| 整段序列的模式 | 更合理的 Q 缩放 | 直觉 |
|----------------|------------------|------|
| 机动剧烈、转弯多 | Q 放大 | 模型（匀速直线等）不准，不确定性大 |
| 匀速直航、平稳 | Q 缩小 | 模型较准，不确定性小 |
| 某一段异常、其余正常 | 需要「看到」整段才能判断 | 单点看不出来是噪声还是真机动 |


### 一个具体例子（直觉）

- **窗口内 5 段**：直 → 直 → 转弯 → 转弯 → 转弯  
  **看整段**：明显在转弯，模型（匀速直线）不对。  
  **结论**：**放大 Q**（这段窗口里少信模型、多信观测）。

- **窗口内 5 段**：直 → 直 → **突然一个怪跳变** → 直 → 直  
  **看整段**：只有中间一段怪，其余一致。  
  **结论**：更像噪声/野值，**不要因为这一段就把 Q 放得很大**，否则会过度不信任模型。

所以：**「注意」其他段，就是为了得到「整段模式」和「这一段在整段里是否异常」**；有了这些，网络才能合理输出缩放因子（Q 该大还是该小）。这就是为什么缩放因子的计算需要去「注意」其他段——**不是为注意而注意，而是因为只有整段信息才能回答「模型在这段时间里可不可信」**。

所以：缩放因子应该是「整段序列」的函数，而不是「最后一个 patch」或「局部平均」的函数。
要实现这一点，模型必须能够看到整段序列并提炼出全局模式。这就是为什么要用 Set-Transformer（自注意力 + PMA）

使用自注意力（SAB）：在 patch 之间交换信息
- Self-Attention：每个 patch 作为 query，去对所有 patch（key/value）做注意力；
- 效果：每个 patch 的表示会被所有其他 patch 加权聚合更新；
- 因此经过 SAB 后，每个 patch 的向量里已经带有「整段序列」的信息（例如「这段窗口里转弯多不多」「前后是否一致」等）

两路输入结合起来的训练作用

传感器数据 x：用来学“当前运动/场景下该怎么调 Q”：
- 通过 Patch Embedding + Set-Transformer + FC 得到一组缩放因子
估计的 $Q̂$
- 作为“基础 Q”：
- 最后一步是 diag(缩放因子) @ Q_slice，再取对角线得到输出。

也就是：网络在 $Q̂$ 上做按维度的缩放，得到最终的 Q。

最后一个框————损失

结合中间存储值，做卡尔曼滤波时，预测步里用的过程噪声协方差不用别的 Q，而用 A-KIT 给出的 Q^A-KIT

目录