目录
state value定义
单步过程
多步trajectory链
return和state value区别
例子
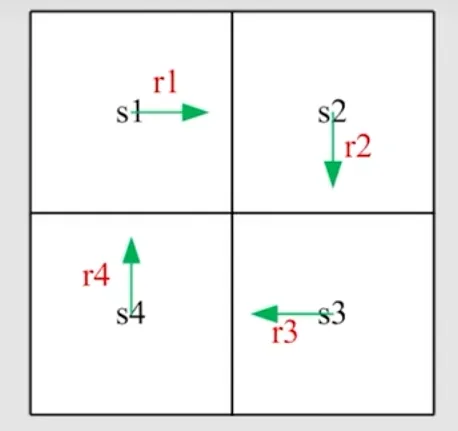
图中有四个状态s1、s2、s3、s4,策略如箭头所示,对应reward是r1、r2、r3、r4,计算从不同状态出发得到的return
用vi表示从不同状态si出发得到的return:
⎩⎨⎧v1v2v3v4=r1+γr2+γ2r3+…=r2+γr3+γ2r4+…=r3+γr4+γ2r1+…=r4+γr1+γ2r2+…
既可以表示成:
v1=r1+γ(r2+γr3+…)=r1+γv2v2=r2+γ(r3+γr4+…)=r2+γv3v3=r3+γ(r4+γr1+…)=r3+γv4v4=r4+γ(r1+γr2+…)=r4+γv1
矩阵形式:
vv1v2v3v4=r1r2r3r4+γv2γv3γv4γv1=rr1r2r3r4+γP0001100001000010vv1v2v3v4
可以表示成:
v=r+γPv
一个状态的value实际上依赖于其他状态的value
state value定义
单步过程
StAtRt+1,St+1
这些跳跃由probability distribution决定
- St→At
- St采取的动作由策略决定 π(At=a∣St=s)
- St,At→Rt+1
- reward probability决定, p(Rt+1=r∣St=s,At=a)
- St,At→St+1
- state transition probability决定, p(St+1=s′∣St=s,At=a)
多步trajectory链
StAtRt+1,St+1At+1Rt+2,St+2At+2Rt+3,…
对其求discounted return:
Gt=Rt+1+γRt+2+γ2Rt+3+…
Rt+2、Rt+3是随机变量,所以Gt也是随机变量
state value是Gt的期望值,即平均值:
vπ(s)=E[Gt∣St=s]
- 是s的函数,从不同的s出发得到的discounted return不同,求平均自然也不同
- 也是策略的函数
- 代表了一种状态的价值,当一个state value较大时,认为该状态比较有价值,即从这个状态出发,会得到更多return
return和state value区别
return针对单个trajectory求出的;state value针对多个trajectory得到的return,再取其平均值
例子
计算状态s1在不同策略下的state value:
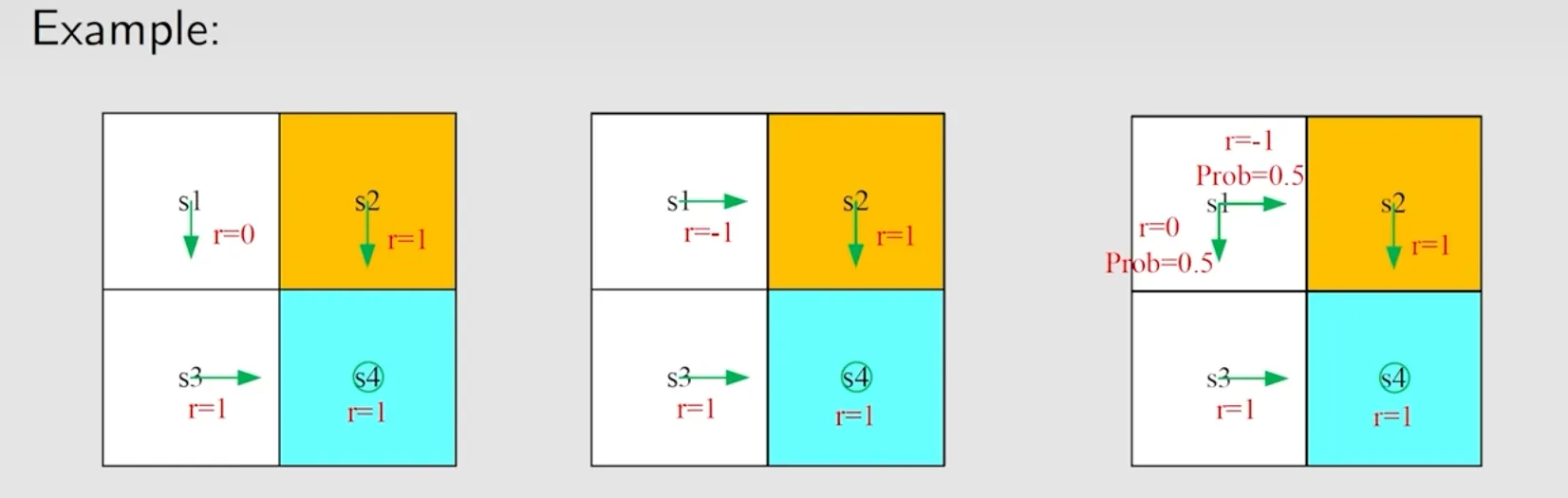
vπ1(s1)=0+γ1+γ21+⋯=γ(1+γ+γ2+…)=1−γγvπ2(s1)=−1+γ1+γ21+⋯=−1+γ(1+γ+γ2+…)=−1+1−γγvπ3(s1)=0.5(−1+1−γγ)+0.5(1−γγ)=−0.5+1−γγ
vπ3有两条trajectory,取平均方法是乘上各自的reward probability
本文作者:cc
本文链接:
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA
许可协议。转载请注明出处!

